【技術】分布活化能模型在生物質熱解動力學中的應用
摘要:文章建立了玉米秸稈熱解反應的分布活化能模型方程,并在此基礎上采用遺傳算法求解實驗值與理論值之,得到誤差最小值,分布活化能模型動力學參數進而得到求解,求得玉米秸稈熱解反應的分布活化能模型方程推導出的預測理論數據。通過實驗測得玉米秸稈熱解反應的熱重數據與建模后所得理論數據進行比較,結果顯示實驗測得數據與模型理論結果擬合度較高,說明此模型適合描述玉米秸稈的熱解反應動力學行為。
生物質能是蘊藏在生物質中的能量,為可再生資源,是潛在的能源和化工原料。生物質材料的熱解是生物質能轉化利用的根本途徑。在煤、生物質等的熱解反應中,各種化學鍵的斷裂呈現出活化能的連續分布,具體到某一特定官能團的反應,由于它們在原有物質結構中所處的位置不同,發生斷裂時所需的活化能也不相同[1]。考慮到生物質原料熱解過程的復雜性,無法通過單一活化能值進行描述,為此,用動力學模型來描述生物質復雜的物理過程,以期深化對其熱解動力學行為的研究。
本文根據阿倫尼烏斯公式建立熱解動力學方程,用Matlab編譯的遺傳算法對實驗值與理論值之差進行求解,得到誤差最小值,進而求解分布活化能模型動力學參數,建立生物質的熱解動力學模型。
01
分布活化能模型的建立
分布活化能模型的研究,最早是源于研究者對煤熱解模型的基礎上提出的。分布活化能模型有兩個假設:一是假設有限多平行反應,反應個數的確定具有經驗性;二是假設無限多的平行反應,則平行的每一階反應活化能可認定呈連續分布。由于生物質的復雜性決定其熱解反應數眾多。假設第i個熱解反應的總揮發量為Vi,直到t時刻揮發的量為Vi,根據假設2,即可得到第i個反應的動力學方程,此方程符合Arrhenius反應定律,但此一階反應模型適用于等溫動力學過程的模擬,不適用于物質組成復雜熱解反應眾多的分布活化能模型中。進而采用微分表示相應的各反應的量,假定各反應頻率因子都一樣,則可得分布活化能模型方程(式(1))。
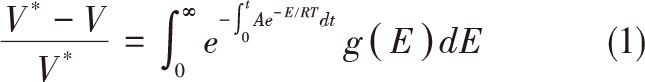
活化能分布函數g(E)通常采用概率論中的概率分布函數表示,一般認為活化能分布為高斯分布函數。式(1)的左邊引入試驗分析中參數,擬合非等溫條件下時間與溫度的關系式,最終得到非等溫Gaussian分布活化能模型方程。但由于存在雙積分無法得出其解析解。而內層dT積分即為熱分析動力學中常見的溫度積分。代入經驗溫度積分式,最終得到
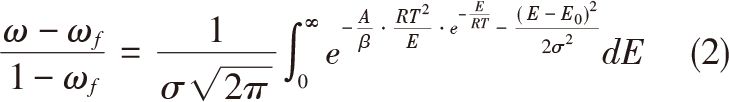
式中A,E0,σ為所求的參數。
傳統的動力學參數求解方法(積分法和微分法)僅對具有單一活化能的模型有效,而且它們的求解存在很大的誤差[2]。本論文采用Matlab中的遺傳算法進行求解。
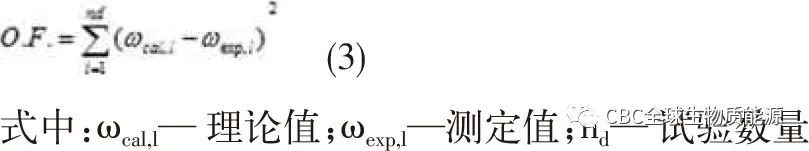
使上述函數達到最小值時的參數值即為所求解參數的過程,實際上轉變成了一個優化問題,運行Matlab中的遺傳算法,即可求出使公式(3)最小值的最優函數,從而求得參數值A,E0,σ的解,E0=125kJ/mol,指前因子A=1.5×109s-1和標準差σ=10kJ/mol。
02
實 驗
以生物質原料為玉米秸稈為例,將事先干燥好的玉米秸稈粉碎成極細的粉末作為實驗物料,對玉米秸稈制取的生物油進行熱重分析,采用Perkin-Elmer熱重分析儀。載氣為高純N2,流量為200ml/min。試樣由室溫在恒定升溫速率(β=15K/min)下加熱至800K,實驗得到熱重曲線,對實驗測得的曲線進行分析。
通過對玉米秸稈試樣熱裂解曲線的分析比較可見,生物質的熱解過程曲線具有三個階段規律。即水分蒸發階段、熱解階段和揮發份持續析出階段。熱解階段的失重最顯著,達到80%~90%,對應的溫度范圍大致為420~800K。這里僅對熱解階段的動力學進行分析,該階段的試驗曲線以及分布活化能模型預測結果與實驗結果的比較見圖1所示。

從圖1中可以看出,此為玉米秸稈的熱解階段,圖中曲線表示為生物質熱解分布活化能模型預測曲線,點表示實驗測定數據。在溫度低于680K時,預測曲線與實驗測定數據擬合得相當好,680K到750K這段有少許偏差,750K之后擬合度也比較高。出現偏差的原因可能是試驗中出現了偶然誤差引起所致,也可能是由于使用的數據點較少,因而求解的活化能數值誤差較大所引起的。總之從總體來看,此分布活化能模型較適合描述玉米秸稈的熱解反應動力學過程,本論文所建立的動力學模型是較合適的。
03
分布活化能模型動力學參數求解結果及活化能分布函數圖形
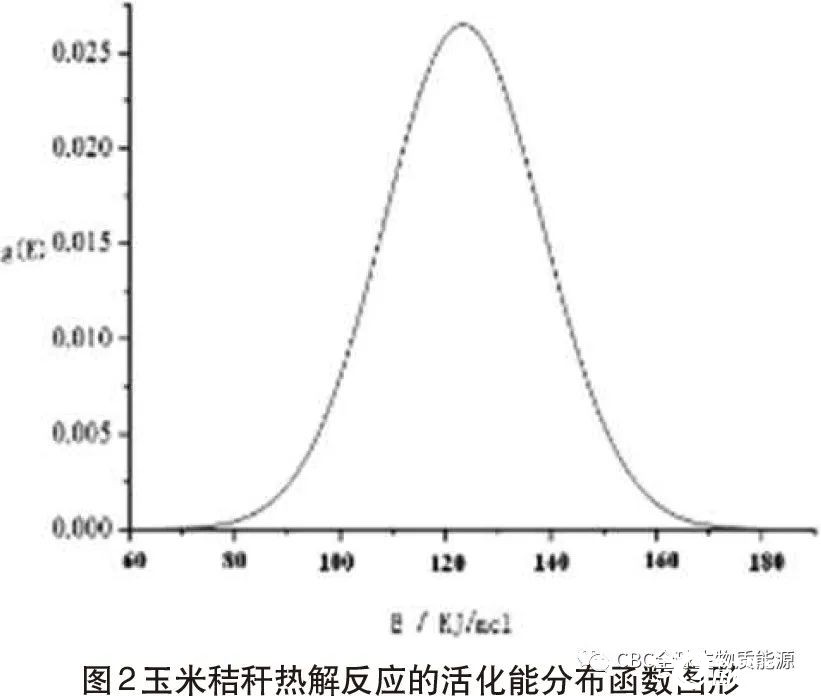
采用非等溫高斯分布活化能模型解析上述動力學分析實驗結果,玉米秸稈熱解反應的活化能分布函數圖形如圖2所示。標準差越小則圖形越窄,說明實驗數據越準確。
04
結 語
生物質原料熱解過程的復雜性,無法通過單一活化能值進行描述。本文推導了生物質熱解反應的分布活化能模型,并將之應用于玉米秸稈的熱解動力學實驗測定結果;采用遺傳算法對實驗值與理論值之差進行求解,得到誤差最小值,進而求解分布活化能模型動力學參數,即反應活化能標準值E0=125kJ/mol,指前因子A=1.5×109s-1和標準差σ=10kJ/mol。進一步給出了相應的分布活化能模型預測曲線,并對兩組數據進行了擬合驗證,結果表明,分布活化能模型較適合描述生物質熱解反應動力學過程。
參考文獻:
[1]劉旭光.煤熱解DAEM模型分析及固定床煤加壓氣化過程[D]太原:中國科學院山西煤炭化學研究所,2000.
[2]胡榮祖,石啟禎.熱分析動力學[M].北京:科學出版社,2000.
以上是小編收集整理的【技術】分布活化能模型在生物質熱解動力學中的應用部分內容來自網絡,如有侵權請聯系刪除:153045535@qq.com;
本文地址:http://www.aa-cctv.com/xinnenyuan/2254.html